- 1924 / Stan. Hakl / Matematické žertíky a paradoxy
„Číslo 37 se povedlo, děti,“ řekl dědeček. „Násobíme-li je čísly 3, 6, 9, 12, 15, 18, 21, 24, 27, obdržíme pokaždé součin, složený ze stejných číslic. Sečteme-li číslice v součinu, dostaneme násobitele. Hleďte!“
37 × 3
111
1 + 1 + 1 = 3
37 × 27
259
74
999
9 + 9 + 9 = 27
Děti se přesvědčily, že dědeček měl pravdu.
- 1924 / Stan. Hakl / Matematické žertíky a paradoxy
Dědeček vyzval Ladíka, aby jakékoliv sedmiciferné číslo znásobil devíti. Chlapec hned v ústraní počítal. Když byl hotov, řekl děd: „Smaž v součinu kteroukoli číslici, pověz mnně zbývající a já ti uhodnu, kterou jsi vymazal.
Láďa předložil dědečkovi součin o jednu číslici zkrácený: 5153888.
Děda sčetl číslice 5 + 1 + 5 + 3 + 8 + 8 + 8=38.
„Které číslo nejbliže vyšší je dělitelno devíti?“
„45.“
„38 a kolik jest 45?“
„7.“
„Vynechal jsi číslici 7.“
Skutečně, neboť Ladík násobil
5726542 × 9
51,538.8(7)8
Tak provedli ještě několik příkladů. Byla-li ze součinu vynechána 0 neb 9, byl součet zbývajících číslic dělitelný devíti a dědeček musil říci: „Buď to byla 9 nebo 0.“
Na př.:
2634523 × 9
23,710.70(7)
2 + 3 + 7 + 1 + 0 + 7 = 20.
7687633 × 9
69,(1)88.697
6 + 9 + 8 + 8 + 6 + 9 + 7 = 53.
I s méněcifernými čísly se pak Láďovi výpočty zdařily.
- 1924 / Stan. Hakl / Matematické žertíky a paradoxy
Nechme zase jednou mluviti číslice!
Násobíme-li kterékoliv číslo od 1 do 10 devítkou a sečteme-li číslice v součinu, máme pokaždé 9.
1 × 9 = 9 . . . + . = 9
2 × 9 = 18 . . 1 + 8 = 9
3 × 9 = 27 . . 2 + 7 = 9
4 × 9 = 36 . . 3 + 6 = 9
5 × 9 = 45 . . 4 + 5 = 9
6 × 9 = 54 . . 5 + 4 = 9
7 × 9 = 63 . . 6 + 3 = 9
8 × 9 = 72 . . 7 + 2 = 9
9 × 9 = 81 . . 8 + 1 = 9
10 × 9 = 90 . . 9 + 0 = 9
- 1924 / Stan. Hakl / Matematické žertíky a paradoxy
Dědeček řekl: „Dovedu i uhodnouti, kolik kdo má peněz v peněžence. Tuhle tatínkovi přepočítejte drobné peníze v tobolce.“ Děd vyšel na chvíli ze světnice a když se vrátil, věděli všichni, že tatínek měl u sebe 36 Kč.
„Tak piš a počítej!“ poručil dědouš Ladíkovi. „Kolik jsi napočítal, násob některým číslem sudým!“
36 × 8 = 288.
„Součin rozděl dvěma!“
288 : 2 = 144.
„Podíl násob opět libovolným sudým číslem!“
144 × 6 = 864.
„Oznam mi součin a řekni také součin obou násobitelů.“
Když se to děd dozvěděl, rozdělil součin nábitelů dvěma a tímto podílem dělil Ladíkem vypočítané číslo.
(8 × 6) = 48, 48 : 2 = 24; 864 : 24 = 36.
Tak uhodl 36 Kč.
- 1924 / Stan. Hakl / Fysika
Dědeček povídal: „Jak rozřešíš, Láďo, následující příklad? Z Prahy do Brna jeden rychlovlak 5 hodin, osobní vlak 10 hodin; jak dlouho tam pojede drožkář?“
Ladík si ovšem nevěděl s příkladem rady.
„Inu, chlapče,“ povídá najednou dědoušek, „to bude záležeti jedině na tom, pojede-li drožkář vlakem osobním, či rychlovlakem. Samozřejmě rychlíkem tam bude dříve.“
Jiného vysvětlení nebylo Láďovi již třeba.
- 1924 / Stan. Hakl / Šikovné ruce
Dnes zavedl dědeček děti do říše bludu a klamu. Položil na stůl papírovou dvacetikorunu a vedle ní desetihaléř. Na bankovce bylo vytištěno šesticiferné číslo.
„Kolik číslic mohu zakrýti desetihaléřem?“ otázal se děd.
„Tři až čtyři,“ hádaly děti.
Dědeček zvedl desetihaléř a zakryl jím celé číslo.
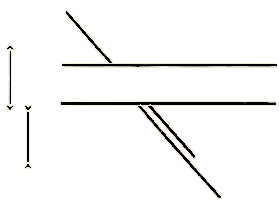
„Zdání klame,“ povídal překvapeným dětem a na doklad nakreslil dva obrázky. „Kdo by na první pohled poznal, že obě úsečky jsou stejně dlouhé, a že kratší přímka pod oběma rovnoběžkami jest pokračováním přímky hoření?“
- 1924 / Stan. Hakl / U nás na vsi
„Dnes stěžoval si mně pan farář, že už i on má svou duši v pekle.“
„V pekle? Opravdu?“
„Opravdu. Jedu vám, povídá, dědečku, ze sousední vsi na kole, na silnici vjedu na hřebík a tu máš, čerte, kropáč, a duše u kola v pekle. Slepovati jí už nelze, a tak musím zítra do Prahy pro novou.“
- 1924 / Stan. Hakl / U nás na vsi
„V Domažlicích byla velkolepá hostina,“ vypravoval děd. „Chodů bylo při ní kromě masa a polévky 156.“
„I pro Pána! Co to všechno jedli?“
„I nic tak zvláštního. Polévku, dvojí maso a moučník. Ale snědli toho hodně; 156 zdravých Chodů něco spořádá.“
„Ach, takových 156 Chodů bylo při obědě, teď rozumím,“ smál se Láďa.
- 1924 / Stan. Hakl / Cizí postavy
Pan Vomáčka odjel na cesty. Před odjezdem řekl své paní, že přijede za pět dní. Avšak obchodní věci vyřídil za den a proto hned telegrafoval, že se mýlil a že přijede dříve.
Na telegrafním úřadě slečna telegrafistka převedla z Morseových znamének tento telegram: „Myl kapři jed udři vepři jedna protivo mačká.“
Paní Vomáčková div nepadla do mdlob, když tu hatlaninu přečetla.
Teprve když se pan Vomáčka vrátil, rozluštil telegram: „Mýlka! Přijedu dříve, přijeď naproti! Vomáčka.“
- 1924 / Stan. Hakl / Cizí postavy
Na panském honě zastřeleno bylo tolik zajíců a koroptví, že bylo dohromady 200 noh a 72 hlavy. Máme vypočítati, kolik bylo zajíců a kolik koroptví. Těžký příklad a podívejte se, jak lehce se dá rozřešiti!
Zajíci a koroptve měli zajisté 72 hlavy. Bylo jich patrně tolikéž kusů. Kdyby každé zvíře mělo po dvou nohách, bylo by úhrnem 144 noh.
Že však bylo 200 noh, čili o 58 více, zavinila patrně čtyřnohost zajíců. Tak připadlo na každého ušáka po dvou přespočetných nohách. 2 v 56 = 28. Bylo tedy 28 zajíců a 44 koroptve.
- 1925 / Stan. Hakl / Matematické žertíky a paradoxy
„A teď něco z počtů,“ oznamoval děd. „Číslo 1863 možno snadno početními výkony proměniti v 9. Sečteme-li první dvě číslice 1 + 8 = 9. Obě ostatní 6 + 3 dají týž součet 9. Sečteme poslední dvě a prvé dvě číslice 63 + 18 = 81. Sečteme-li číslice součtu 8 + 1 obdržíme 9. Dělíme-li součet devíti, dostaneme podíl 9. 81 : 9 = 9. Odečteme-li naproti tomu 18 od 63, zbyde 45. 4 + 5 = 9. Dělíme-li 63 : 18 = 3 a zbytek je zase 9. Násobíme-li všecky číslice dohromady 1 × 8 × 6 × 3, obdržíme 144, čili 1 + 4 + 4 = 9. Dělíme-li 1863 : 9 = 207. Sečteme-li číslice v podílu 2 + 0 + 7 = 9. Tedy devět a zase devět a kdo nevěří je medvěd, jako v tom prostonárodním říkadle,“ zakončil dědoušek.
- 1925 / Stan. Hakl / Fysika
Dědeček položil na okraj stolu staré pořezané pravítko a přikryl je dobře přiléhající vrstvou novin a udeřiv pěstí na jeho přečnívající část, přerazil je jako nic. Tenký novinový papír svou širokou plochou zadržel při úderu přikrytou jím část pravítka, že se ani nepohnula. Dědeček je tak přelomil lehčeji, než kdyby je přehýbal přes koleno. Zkuste a uvidíte. Může to však býti i jiné prkénko. Dobrého pravítka škoda!
- 1925 / Stan. Hakl / Kouzelnické kousky
„Abych vám, děti, dokázal, že dovedu uhodnouti i myšlénku, posaďte se tuhle vedle sebe pěkně do řady. Držte v ruce tužku, jíž jste právě kreslily. — Tak.“
Dědeček odebral tužku Mařence, pak Jeníkovi, Amálce i Vašíkovi. Naposled přiblížil se k Ladíkovi. „Vím,“ povídal, „Ladík si teď myslí, že i jemu tužku odejmu. Mýlíš se však, holečku! Stačí když vím, co si právě myslíš.“
A Ladík nezapřel, že i tentokrát dědeček uhodl.
- 1925 / Stan. Hakl / Šibalství s penězi
Dědeček povídal: „Haléř je nerozměnitelný. Dvouhaléř lze rozměniti pouze jednou ve dva haléře. Pětihaléř rozměníme třikrát: v pět haléřů, v jeden dvouhaléř a tři haléře, ve dva dvouhaléře a jeden haléř. Desetihaléř pětkrát: v deset haléřů, v jeden dvouhaléř a 8 haléřů, ve 2 dvouhaléře a 6 haléřů, ve 3 dvouhaléře a 4 haléře, ve 4 dvouhaléře a 2 haléře. Korunu můžeme rozměniti 3.953krát. Máte chuť všecky způsoby přepočítati? Já dnes ne.“
- 1925 / Stan. Hakl / Dědeček vypravuje
„Pamatuješ se, Ladíku, na ty ocelové hodinky, které jsem před dvěma roky ztratil?“
„Pamatuji se, tenkrát jste všchno prohledal a přec jste jich nenašel,“ odvětil Ladík dědečkovi.
„Nuže, včera jsem oblékl starou vestu, které jsem již neměl dlouho na sobě, a co bys myslil, že jsem našel v kapse?“
„Ztracené hodinky,“ zvolal hoch.
„Nikoliv,“ vece děd, „našel jsem díru, kterou hodinky vypadly.“
- 1925 / Stan. Hakl / Hádanky
Ladík četl pověsti o vodníkovi. Dědeček seděl u stolu a kouřil a poslouchal. Najednou povídá: „A víš-li pak, hochu, jak povstal vodník?“
„Že nevíš? Inu — takhle!“ Zvedl se od stolu a odešel.
- 1926 / ? / Matematické žertíky a paradoxy
„Kytička konvalinek jest v Praze na předměstí za 2 koruny. Co stojí na Václavském náměstí?“ ptal se děd.
„A že to nevíte, děti?“ divil se. „Na Václavském náměstí stojí pomník svatého Václava, chytráci!“
- 1926 / Stan. Hakl / Matematické žertíky a paradoxy
Když se v naší domácnosti objevil nový kalendář, upozornil dědeček na mnohé jeho zajímavosti:
Obyčejný rok se končí vždy týmž dnem v týdnu, kterým započal.
Duben se počíná v týž den, jako červenec, září a prosinec.
Únor, březen i listopad se počínají v tentýž den týdne.
Pravidlo toto se ovšem nevztahuje na roky přestupné.
Žádné století nemůže se začít ve středu, v pátek nebo v sobotu.
Kalendář se vždy za 28 let opakuje.
Kalendář — starý lhář, praví sice české pořekadlo, ale v těchto případech nikdy nezalže, to si pamatujte, děti.
- 1926 / Stan. Hakl / Zeměpis
„V Japonsku milují rodiče své děti tak, že je dokonce poslouchají.“
„Opravdu?“
„Zajisté. A jak rádi poslouchají rodiče své děti, když jim tyto něco pěkného vypravují.“
- 1926 / Stan. Hakl / Přírodozpyt
„Víte-li pak, děti, proč má žirafa tak dlouhý krk?“ ptal se dědeček dětí.
„Inu, protože má tak vysoko hlavu,“ vysvětloval s úsměvem.

