Původní anekdoty
Dle ročníku - 1924 (celkem 16):
- 1924 / ? / Šikovné ruceDědeček se mrzel, opravdu se mrzel — a to bylo špatné znamení, že by dětem pověděl některý ze svých žertů! Kdosi přelezl mříž, která chránila jeho zahrádku, a otrhal mu do rána jablka. Proto byl dědeček mrzut.
„Co se stalo, dědečku?“
Dědeček vzal kus papíru a kreslil záhadnou mříž, psal pod ní písmena:
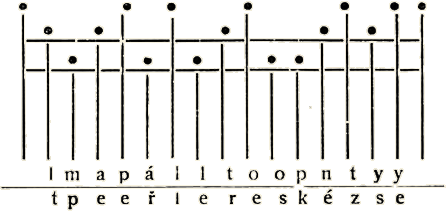
Děti nestrhly očí. „Co to znamená? Vysvětlete nám!“ volaly nedočkavě.
„Čtěte písmena dle délky přímek a zvíte, co mě mrzí!“ pravil dědeček.
Kdo první rozluští záhadu? - 1924 / J. Janoušek / Cizí postavyO čem fysika nemluví.
Na záhořské jednotřídce táže se pan učitel dospělejších žáků po látkách, které se hojně vypařují. Správné odpovědi, že jsou to hlavně líh, čpavek, éther a podobné, odměňuje pochvalou. Té chce být účasten i Čmuchálkův Jára, synek řezníkův, nejmenší z nováčků. Hlásí se tedy velmi naléhavě k odpovědi. A když se dostane k slovu, zapiskne teničkým hláskem: „A taty pjasata se ojne vypazují!“ - 1924 / Stan. Hakl / U nás na vsi„Dnes stěžoval si mně pan farář, že už i on má svou duši v pekle.“
„V pekle? Opravdu?“
„Opravdu. Jedu vám, povídá, dědečku, ze sousední vsi na kole, na silnici vjedu na hřebík a tu máš, čerte, kropáč, a duše u kola v pekle. Slepovati jí už nelze, a tak musím zítra do Prahy pro novou.“ - 1924 / Stan. Hakl / Esence sivého čtveráctvíDědeček byl u dcery v Praze na návštěvě. Seděl uprostřed klubíčka svých vnoučků, když se náhle zvenčí ozvalo hlasité: „Cing, ciling, cililing.“
Zvedl prudce hlavu, poslouchá a povídá: „Na copak to zvoní?“
„Na popel,“ poučovaly děti.
„Na popel? I heleďme! U nás v Makotřasích pořád ještě zvoní na zvonec.“ - 1924 / Stan. Hakl / Matematické žertíky a paradoxyNa panském honě zastřeleno bylo tolik zajíců a koroptví, že bylo dohromady 200 noh a 72 hlavy. Máme vypočítati, kolik bylo zajíců a kolik koroptví. Těžký příklad a podívejte se, jak lehce se dá rozřešiti!
Zajíci a koroptve měli zajisté 72 hlavy. Bylo jich patrně tolikéž kusů. Kdyby každé zvíře mělo po dvou nohách, bylo by úhrnem 144 noh.
Že však bylo 200 noh, čili o 58 více, zavinila patrně čtyřnohost zajíců. Tak připadlo na každého ušáka po dvou přespočetných nohách. 2 v 56 = 28. Bylo tedy 28 zajíců a 44 koroptve. - 1924 / Stan. Hakl / Matematické žertíky a paradoxyDěd napsal liché číslice ve třech svislých řadách.
111
333
555
777
999
„Mám smazati všecky číslice kromě tří, aby součet činil 20. Dívejte se, jak to provedu!“
.11
...
...
...
..9
.20 - 1924 / Stan. Hakl / Matematické žertíky a paradoxy„Pozor, Láďo! Napiš si čtyřciferné číslo, a uhodnu ti je.“
Ladík napsal 3682.
„Násob první číslici na levo dvěma a připočti 5. Násob pěti a připočti 10. K součtu připočítej druhou číslici. Násob opět desíti. K součinu přidej třetí číslici a znovu násob deseti. Připočti poslední číslici a pověz mi, kolik jsi vypočítal.“
Děd odečetl 7182.
Láďa hlásil 3500.
Rozdíl činil původní číslo 3682.
Bylo-li původní číslo pěticiferné, odečetl děd 35.000 od Ladíkova výpočtu, při čísle šesticiferném 350.000, sedmiciferném 3,500.000 atd.
Přesvědčte se a počítejte! - 1924 / Stan. Hakl / Matematické žertíky a paradoxy„Číslo 37 se povedlo, děti,“ řekl dědeček. „Násobíme-li je čísly 3, 6, 9, 12, 15, 18, 21, 24, 27, obdržíme pokaždé součin, složený ze stejných číslic. Sečteme-li číslice v součinu, dostaneme násobitele. Hleďte!“
37 × 3
111
1 + 1 + 1 = 3
37 × 27
259
74
999
9 + 9 + 9 = 27
Děti se přesvědčily, že dědeček měl pravdu. - 1924 / Stan. Hakl / Cizí postavyPan Vomáčka odjel na cesty. Před odjezdem řekl své paní, že přijede za pět dní. Avšak obchodní věci vyřídil za den a proto hned telegrafoval, že se mýlil a že přijede dříve.
Na telegrafním úřadě slečna telegrafistka převedla z Morseových znamének tento telegram: „Myl kapři jed udři vepři jedna protivo mačká.“
Paní Vomáčková div nepadla do mdlob, když tu hatlaninu přečetla.
Teprve když se pan Vomáčka vrátil, rozluštil telegram: „Mýlka! Přijedu dříve, přijeď naproti! Vomáčka.“ - 1924 / Stan. Hakl / Matematické žertíky a paradoxyDědeček vyzval Ladíka, aby jakékoliv sedmiciferné číslo znásobil devíti. Chlapec hned v ústraní počítal. Když byl hotov, řekl děd: „Smaž v součinu kteroukoli číslici, pověz mnně zbývající a já ti uhodnu, kterou jsi vymazal.
Láďa předložil dědečkovi součin o jednu číslici zkrácený: 5153888.
Děda sčetl číslice 5 + 1 + 5 + 3 + 8 + 8 + 8=38.
„Které číslo nejbliže vyšší je dělitelno devíti?“
„45.“
„38 a kolik jest 45?“
„7.“
„Vynechal jsi číslici 7.“
Skutečně, neboť Ladík násobil
5726542 × 9
51,538.8(7)8
Tak provedli ještě několik příkladů. Byla-li ze součinu vynechána 0 neb 9, byl součet zbývajících číslic dělitelný devíti a dědeček musil říci: „Buď to byla 9 nebo 0.“
Na př.:
2634523 × 9
23,710.70(7)
2 + 3 + 7 + 1 + 0 + 7 = 20.
7687633 × 9
69,(1)88.697
6 + 9 + 8 + 8 + 6 + 9 + 7 = 53.
I s méněcifernými čísly se pak Láďovi výpočty zdařily. - 1924 / Stan. Hakl / Šikovné ruceDnes zavedl dědeček děti do říše bludu a klamu. Položil na stůl papírovou dvacetikorunu a vedle ní desetihaléř. Na bankovce bylo vytištěno šesticiferné číslo.
„Kolik číslic mohu zakrýti desetihaléřem?“ otázal se děd.
„Tři až čtyři,“ hádaly děti.
Dědeček zvedl desetihaléř a zakryl jím celé číslo.
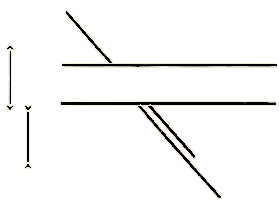
„Zdání klame,“ povídal překvapeným dětem a na doklad nakreslil dva obrázky. „Kdo by na první pohled poznal, že obě úsečky jsou stejně dlouhé, a že kratší přímka pod oběma rovnoběžkami jest pokračováním přímky hoření?“ - 1924 / Stan. Hakl / FysikaDědeček povídal: „Jak rozřešíš, Láďo, následující příklad? Z Prahy do Brna jeden rychlovlak 5 hodin, osobní vlak 10 hodin; jak dlouho tam pojede drožkář?“
Ladík si ovšem nevěděl s příkladem rady.
„Inu, chlapče,“ povídá najednou dědoušek, „to bude záležeti jedině na tom, pojede-li drožkář vlakem osobním, či rychlovlakem. Samozřejmě rychlíkem tam bude dříve.“
Jiného vysvětlení nebylo Láďovi již třeba. - 1924 / Stan. Hakl / Matematické žertíky a paradoxyNechme zase jednou mluviti číslice!
Násobíme-li kterékoliv číslo od 1 do 10 devítkou a sečteme-li číslice v součinu, máme pokaždé 9.
1 × 9 = 9 . . . + . = 9
2 × 9 = 18 . . 1 + 8 = 9
3 × 9 = 27 . . 2 + 7 = 9
4 × 9 = 36 . . 3 + 6 = 9
5 × 9 = 45 . . 4 + 5 = 9
6 × 9 = 54 . . 5 + 4 = 9
7 × 9 = 63 . . 6 + 3 = 9
8 × 9 = 72 . . 7 + 2 = 9
9 × 9 = 81 . . 8 + 1 = 9
10 × 9 = 90 . . 9 + 0 = 9 - 1924 / Stan. Hakl / U nás na vsi„V Domažlicích byla velkolepá hostina,“ vypravoval děd. „Chodů bylo při ní kromě masa a polévky 156.“
„I pro Pána! Co to všechno jedli?“
„I nic tak zvláštního. Polévku, dvojí maso a moučník. Ale snědli toho hodně; 156 zdravých Chodů něco spořádá.“
„Ach, takových 156 Chodů bylo při obědě, teď rozumím,“ smál se Láďa. - 1924 / Stan. Hakl / Matematické žertíky a paradoxyDědeček řekl: „Dovedu i uhodnouti, kolik kdo má peněz v peněžence. Tuhle tatínkovi přepočítejte drobné peníze v tobolce.“ Děd vyšel na chvíli ze světnice a když se vrátil, věděli všichni, že tatínek měl u sebe 36 Kč.
„Tak piš a počítej!“ poručil dědouš Ladíkovi. „Kolik jsi napočítal, násob některým číslem sudým!“
36 × 8 = 288.
„Součin rozděl dvěma!“
288 : 2 = 144.
„Podíl násob opět libovolným sudým číslem!“
144 × 6 = 864.
„Oznam mi součin a řekni také součin obou násobitelů.“
Když se to děd dozvěděl, rozdělil součin nábitelů dvěma a tímto podílem dělil Ladíkem vypočítané číslo.
(8 × 6) = 48, 48 : 2 = 24; 864 : 24 = 36.
Tak uhodl 36 Kč. - 1924 / Stan. Hakl / Cizí postavyNa panském honě zastřeleno bylo tolik zajíců a koroptví, že bylo dohromady 200 noh a 72 hlavy. Máme vypočítati, kolik bylo zajíců a kolik koroptví. Těžký příklad a podívejte se, jak lehce se dá rozřešiti!
Zajíci a koroptve měli zajisté 72 hlavy. Bylo jich patrně tolikéž kusů. Kdyby každé zvíře mělo po dvou nohách, bylo by úhrnem 144 noh.
Že však bylo 200 noh, čili o 58 více, zavinila patrně čtyřnohost zajíců. Tak připadlo na každého ušáka po dvou přespočetných nohách. 2 v 56 = 28. Bylo tedy 28 zajíců a 44 koroptve.
<< < 1 > >>
